Interference of Light Waves and Young’s Double Slit Experiment

Interference of Light Waves :-

When two light waves from different sources meet together, then the distribution of energy due to one wave is distributed by the other. This modification of light energy due to superposition of two light wave is called interference of light waves.

Coherent sources :-

Those sources of light which emit light waves continuously of same wavelength, time period, frequency, amplitude and have zero phase difference or constant phase difference are coherent sources.

Interference of light waves may be of

Two types –

1. Constructive Interference.
2. Destructive Interference.

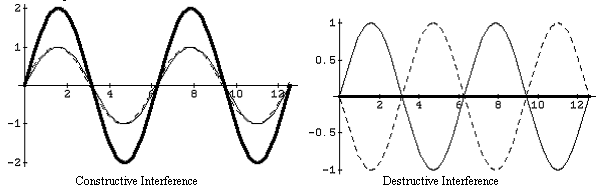
Constructive Interference :-

When two light waves are superpose with each other in such a way that the crest of one wave falls on the second wave and through of one wave falls on the through of the second wave, then the resultant wave has larger amplitude and it is called constructive interference.

Destructive Interference :-

When two light waves superpose with each other in such a way that the crest of one wave coincides through of the second wave, then the amplitude, intensity of resultant wave becomes zero and it is called destructive interference.

Essential conditions for Constructive Interference :-

1. For Constructive Interference phase difference of the waves at the point should be even multiple of π

i. e φ = 0, +2π, -2π, +4π, -4π, +8π, -8π ……

Or

φ = +2nπ, -2nπ

where n = 0, 1, 2, …..

2. For Constructive Interference path difference of the waves should be even multiple of λ/2

If light sources S₁ and S₂ , distance from the point P is y₁ and y₂ respectively, then the path deference

∆P = S₁P – S₂P = y₂ – y₁

Since the value of phase difference between separate two points from λ distance 2π

Hence the phase difference for ∆P path difference

φ = (2π/λ) ∆P

We know that φ = 2πn

Hence (2π/λ) ∆P =2nπ

∆P = nλ

Or

∆P = 2nλ/2

3. For Constructive Interference the resultant Intensity should be maximum.

For maximum Intensity

cosφ = +1

If the displacement produced by The source S₁ and S₂ at the point P is given by

y₁ = a cosωt

y₂ = a cosωt

Then the resultant displacement at Point P would be given by

y = y₁ + y₂ = 2 a cosωt

Since the Intensity is proportional to the square of the amplitude, the resultant Intensity will be given by

I = 4I₀

Where I₀ is the Intensity of each source and I₀ proportional a²

Essential conditions for Destructive Interference :-

1. For Destructive Interference phase difference of the waves at a point should be odd multiple of π

i. e φ = +π, -π, +3π, -3π, +5π, -5π, +7π, -7π …..

Or

Φ = (2n +1)π

where n =0, 1, 2, 3, ….

2. For Destructive Interference path difference of the waves at a point should be odd multiple of λ/2

φ = (2n +1)π

The phase difference ∆P path difference

φ = (2π/λ)∆P

= (2n +1) π

Or

∆P = (n + 1/2) λ

Or

∆P = (2n +1) λ/2

3. For Destructive Interference the resultant Intensity should be minimum.

For minimum Intensity

cosφ = -1

For Destructive Interference the resultant Intensity will be zero.

Young’s Double Slit Experiment :-

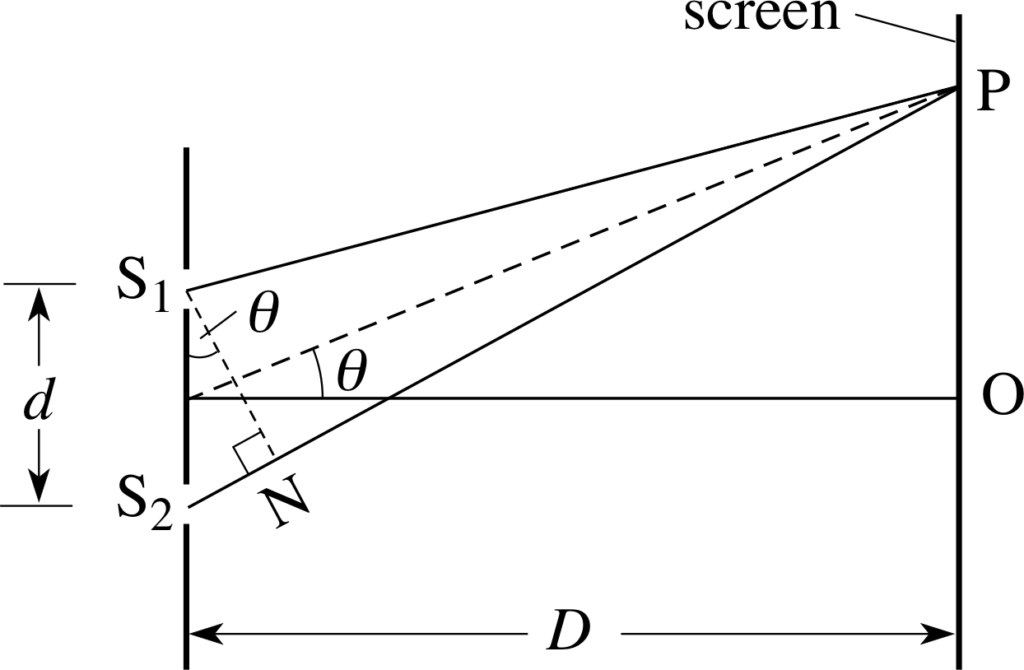
Young’s performed an experiment to prove the wave nature of Light by explaining the phenomenon of interference. He used to coherent sources to perform in this experiment.

He used a light bulb, two small slits S₁ and S₂ , Source S .

Here in the above figure, we and say that the slits are placed very close to each other and are separated by the distance d.

There is a screen placed in front of the setup. He observed that alternate dark and light bands were formed on the screen, such bands are called fringes.

• The source S illuminate the Source S₁ and S₂ therefore the light from S₁ and S₂ becomes coherent because both S₁ and S₂ receive their light from same source S . So if there is any change in the phase, the change will reflect in both S₁ and S₁ when both the slits are open, fringes are formed.

• We can say that S₁ and S₂ will always remain in phase. In the double slit experiment consecutive bright as well as dark fringes are seen on the screen as a consequence of the type of interference of light waves.

• The Interference fringe minimum occur for Path difference = (2n +1)λ

• The Interference fringe maximum occur for path difference = nλ