Huygens’s Wave Theory :-
Scientist Christian Huygens in 1678 found that light is a form of wave, He found that light propagates in the form of waves and need a medium to propagate in all possible direction, he proposed a theory of wave called Huygens’s wave theory.
He told that the secondary source which is obtained from the wavefront of first source give rise to new wavelets and the tangent down to combine all individual wavefronts formed by wavelets of secondary source forms secondary wavefront.

When applied to the propagation of light waves,
Huygens’s wave theory states that every point on a wavefront may be considered a source of secondary spherical wavelets which spread out in the forward direction at the speed of light. The new wavefront is the tangential surface to all of the secondary wavelets.
Huygens’s wave theory of light is differ from Newton’s Corpuscular theory. Newton proposed this theory that treats light as being composed of tiny particles. We use this Theory to describe reflection, refraction, secondary rainbow and primary rainbow. It cannot explain the interference diffraction and polarization.
Huygens’s wave theory of light used to describe reflection, refraction, secondary and primary rainbow, interference, diffraction and polarization of light.
Wavefront :-
The set of points in space reached by a wave or vibration at the same instant as the wave travels through a medium.
Wavefronts generally form a continuous line or Surface.
Types of wavefronts :-
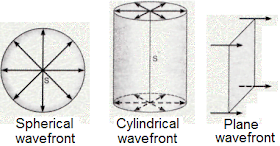
(a) Spherical Wavefront :-
A wavefront originating from the point source of light at the finite distance is called spherical wavefront.
(b) Plane Wavefront :-
As time passes the spherical surface of spherical wavefront is so large that is a small part of it can be considered as a plane wavefront.
A wavefront originating from the point source of light at infinite distance i. e. at very large distance is called as plane wavefront.
(c) Cylindrical wavefront :-
A wavefront originating from a linear source of light is called cylindrical wavefront.
Refraction of plane waves using Huygens’s Wave Theory :-

Let v₁ and v₂ represent the speed of light in medium 1 and medium 2 respectively.
Let t be the time taken by the wavefront to travel the distance BC.
Thus BC = v₁ t
we draw a sphere of radius v₂ from the Point A in the second medium.
Then AE = v₂ t
Now from triangle ABC and AEC
sin i = BC / AC = v₁t / AC
sin r = AE / AC = v₂t / AC
Where i and r are the angles of incidence and refraction respectively.
We obtained
sin i / sin r = v₁ t x AC / AC x v₂ t = v₁ / v₂
i. e. sin i / sin r = v₁ / v₂
If c represents the speed of light in vacuum then refractive index
μ₁ = c / v₁
μ₂ = c / v₂
Now from Snell’s Law of Refraction we can write
μ₁ sin i = μ₂ sin r
If λ₁ and λ₂ denotes the wavelengths of light in medium 1 and medium 2 respectively and distance
ΒC = λ₁
ΑΕ = λ₂
Thus λ₁ / λ₂ = BC /AE = v₁ / v₂
Or v₁ / λ₁ = v₂ / λ₂
Reflection of plane Waves using Huygens’s Wave Theory :-

considered a plane wave AB incident at an angle i on a reflecting surface MN.
If v represents the speed of the wave in the medium and if t represents the time taken by the wavefront to advance from the point B and C then the distance
BC = v t
In order the Construct reflected wavefront we draw a sphere of radius v t from the point A.
Let CE represent the tangent plane drawn from the point C to this sphere.
Obviously
AE = BC = v t
If we now consider the triangles EAC and BAC we will find that they are congruent and therefore, the angles i and r would be equal. This is the law of reflection.
i. e. ∠i = ∠r
Refraction from plane Wave by a thin prism, a convex lens and Reflection by a concave mirror :-

(a) Consider a plane wave passing through a thin prism, clearly, since the speed of light waves is less in class, the lower portion of the incoming wavefront will get delayed resulting in a tilt in the emerging wavefront.
(b) We consider a plane wave incident on a thin convex lens, the central part of the incident plane wave traverses the thickest portion of the lens and is delayed the most. Emerging wavefront depression at the centre and therefore the wavefront becomes spherical and converges to the point F which is known as the focus.
(c) In the above figure a plane wave is incident on a concave mirror and on reflection we have a spherical wave conversion to the focal point F.
we can understand refraction and Reflection by concave lenses and convex mirrors.