Diffraction of Light :-
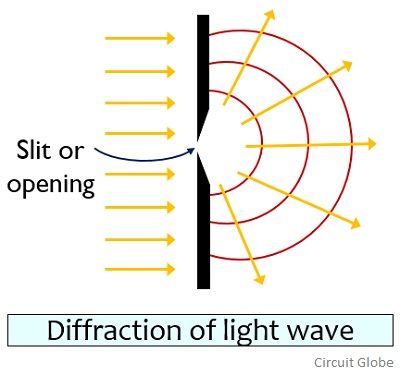
Diffraction of light is the slight bending of light as it passes around the edge of an object. The amount of bending depends on the relative size of the wavelength of light to the side of the opening.
- Italian scientist Francisco Maria Grimaldi coined the word diffraction of light and was the first to record accurate observations of the phenomenon in 1660.
- If the opening is much larger than the light’s wavelength, the bending will be almost unnoticeable. However, if the two are closer in size or equal to the amount of bending is considerable and easily seen with the naked eye.
- Diffraction of light is a general characteristic exhibited by all types of waves such as sound waves, light waves, water waves or matter waves.
- A single narrow slit acts as a new source from which light spreads out. Before Young’s experiment, Newton had noticed that light spreads out from narrow holes or slits. It seems to turn around corners and enters regions where we would expect a shadow, these effects known as diffraction of light.
Explanation of the Intensity distribution in the diffraction pattern :-
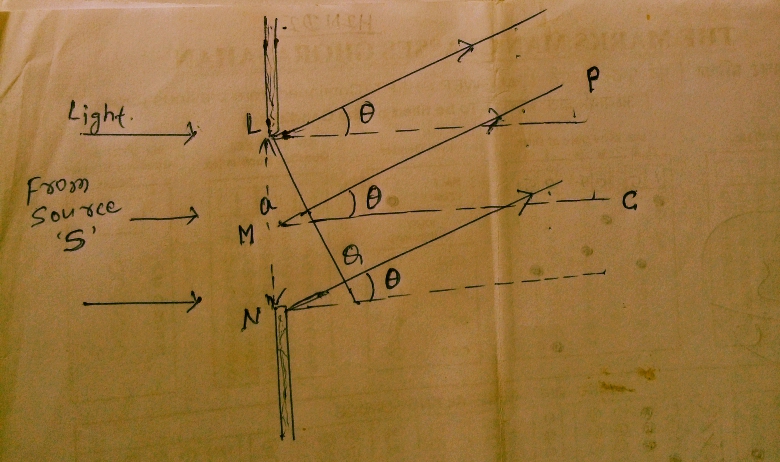
Figure shows a parallel beam of light falling normally on a single slit LN of width ‘a‘
The diffracted light goes on to meet a Screen. The midpoint of the slit is ‘M’
A straight line through M perpendicular to the slit plane meets the screen at ‘C’
We want the intensity at any point ‘P’ on the screen. As before straight lines in joining P to the different points L, M, N etc. can be treated as a parallel making an angle θ with a normal MC.
The path difference NP – LP between the two edge of the Slit can be calculated exactly as for Young’s experiment.
NP – LP = NQ = a sinθ
Or λ = a sinθ
For θ → 0
NP – LP = a θ
i. e λ = a θ
At the Central Point C on the screen, the angle θ is zero. All path differences are zero and hence all the parts of the slit contribute in phase, this gives maximum Intensity at C.
Experiment observations shown in the figure indicates that the intensity has a central maximum at θ = 0
Distinction between Interference and Diffraction of Light :-
Interference of Light :-
- Two separate wave fronts originating from two coherent sources produce Interference.
2. The region of minimum Intensity is perfectly dark in Interference.
3. Width of the fringes is equal in Interference.
4. The Intensity of all position of maxima are of the same Intensity in Interference.
Diffraction of Light :-
- Secondary wavelets originating from different parts of the same wavefront constitute diffraction.
2. In diffraction they are not perfectly dark.
3. In diffraction they are never equal.
4. In diffraction they do vary.
Note :- Interference and diffraction, light energy is redistributed. If it reduces in one region, producing a dark fringe. It increases in another region, producing a bright fringe. There is no gain or loss of energy which is consistent with the principle of conservation of energy.
Fresnel Distance :-

An aperture (slit) of size ‘a’ illuminated by a parallel beam sends diffracted light into an angle of approximately = λ/a
This is the angular size of bright and central Maxima.
In traveling a distance Z the diffracted beam therefore acquires a width Zθ
Zθ = Zλ/a
If width of beam is equal to the size of aperture
then Z = a²/λ
We define a quantity Zf called the Fresnel distance by the following equation
Zf = a²/λ
Question :- For what distance is ray optics a good approximation when the aperture is 3 mm wide and the wavelength is 500 nm ?
Zf = a²/λ = (3 x 10⁻³) / 5 x 10⁻⁷ = 18 m