Radioactivity :-
Henry Becquerel discovered radioactivity in 1896 by accident.
Experiments performed subsequently showed that radioactivity was a nuclear phenomenon in which an unstable nucleus undergoes a decay.
Becquerel studying the fluorescence and phosphorescence of compounds irradiated with visible light, the observed an interesting phenomenon. After illuminating some pieces of uranium-potassium sulphate with visible light he wrapped them in black paper and separated the package from a photographic plate by a piece of silver.
When after several hours of exposure, the photographic plate was affected, it showed blackening due to something that must have been emitted by the compound and was able to penetrate both black paper and the silver.
This is referred to as a radioactive decay.
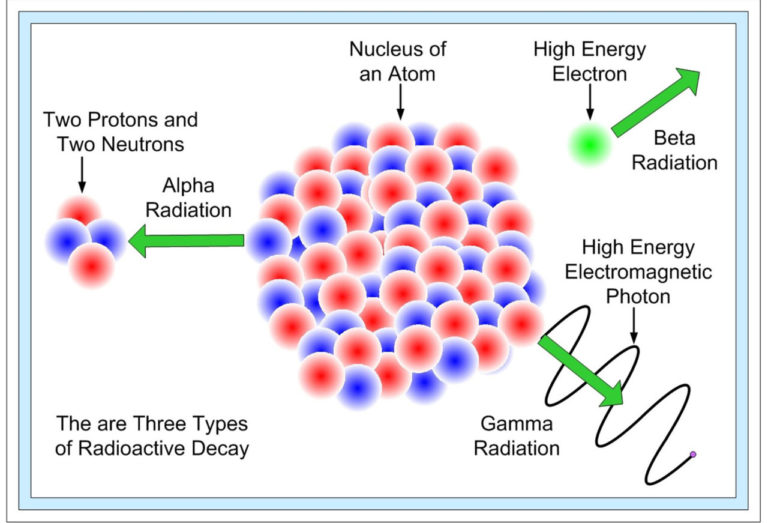
Three types of radioactive decay occurs in nature –
(1) Alpha decay.
(2) Beta decay.
(3) Gamma decay.
- Those substance who emits alpha, beta and gamma rays, the substance is called radioactive.
Examples – uranium, thorium, radium actenium etc.
- The radioactive substance radium was discovered by Madam Curie and her husband Pierre Curie in 1898.
- Properties of radioactivity in radium (Rm) is more (40 times) than the uranium but less than the polonium (Po).
Law of Radioactive Decay :-
In any radioactive sample, which undergoes alpha, beta or Gamma decay. It is found that the number of nuclei undergoing the decay per unit time is proportional to the total number of nuclei in the sample.
If N is the number of nuclei in the sample and ∆N undergo decay in time ∆t then
∆N/∆t proportional N
∆N/∆t = ∧ N
Where ^ is called radioactive decay disintegration constant.
- If the limit ∆t → 0
then the rate of change of N is
∆N/∆t = – ∧ dt
or
∆N/N = -^ dt
- ∆N is the number of nuclei that decay and hence is always positive, but dN is the change in N, here it is negative.
- Now integrating both sides of the above equation, we get
∫ dN/N = -^∫dt
or In N – In N₀ = -^ (t – t₀)
Here N₀ is the number of radioactive nuclei in the sample at Some orbitary time t₀ and N is the number of radioactive nuclei at any subsequent time t.
If t₀ = 0
Then In N/N₀ = -^ t
Which gives N(t) = N₀e⁻^ t
- The total decay rate R of a sample in the number of nuclei disintegrating per unit time.
Suppose in a time interval dt, the decay count measured is ∆N
Then dN = -∆N
The positive quantity R is then defined as
R = -dN/dt
Differentiating equation
N(t) = -N₀e⁻^t
We find R = -dN/dt = ^N0e⁻^t
or
R = R₀e⁻^t
Where R₀ = ^ N₀ at t = 0
This is equation to the law of radioactive decay.
The decay rate at time t and the number of undecayed nuclei N is given by
R = ^ N
The SI unit of decay rate is Becquerel (Bq).
There is another unit named ‘Curie’ that is widely used and is related to SI unit
1 Curie = 3·7 × 10¹⁰ Bq











