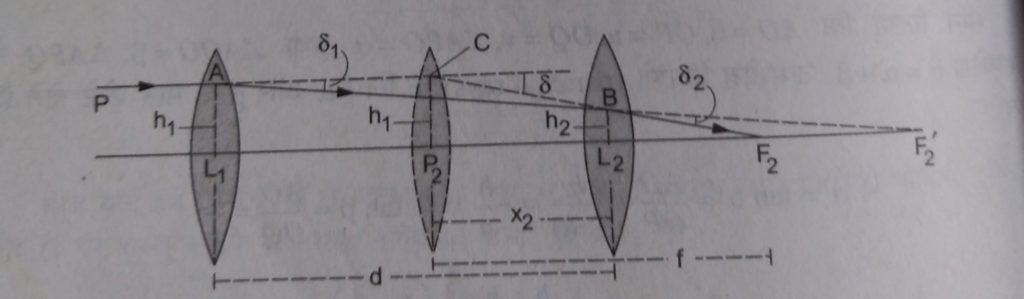
Equivalent focal length of two lenses :- Let us consider two lenses L₁ ( focal length f₁ ) and L₂ ( focal length f₂ ) are separated by a distance d and P₂ is equivalent lens of both lenses ( focal length f ). Angle of deviation produce by the lenses P, L₁ and L₂ are δ, δ₁ and δ₂ respectively, then from the above figure.
δ = δ₁ + δ₂
h₁/f = h₁/f₁+ h₂/f₂ ………….( 1)
From ∆ AL₁F₂’ and ∆ BL₂F₂’
AL₁/L₁F₂’ = BL₂/L₂F₂’
AL₁/L₁F₂’ = BL₂/L₁F₂- L₁L₂
h₁/f₁ = h₂/f₁ – d
Hence, h₂ = h₁( f₁- d )/f₁
Put the value of h₂ in equation ( 1 )
h₁/f = h₁/f₁ + h ( f₁ – d )/f₁f₂
1/f = 1/f₁ + ( f₁ – d )/f₁f₂
1/f = 1/f₁ + 1/f₂ – d/f₁f₂
Hence, f = f₁f₂/f₁ + f₂ – d …………….. ( 2 )
Position of equivalent lens :-
From ∆ CP₂F₂ and ∆ BL₂F₂
P₂F₂/L₂F₂ = CP₂/BL₂
f/f – x₂ = h₁/h₂
Here P₂F₂ = f
According to the sign convention
f/f – ( – x₂ ) = h₁/h₂
f/f + x₂ = h₁/h₂
since, h₂ = h₁ ( f₁ – d )/f₁
hence, f/f + x₂ = f₁/f₁ – d
or ff₁ – fd = ff₁ + x₂f₁
or x₂ = – fd/f₁
From equation ( 2 )
or x₂ = – f₁f₂d/f₁ + f₂ – d f₁
or x₂ = -f₂d/f₁ + f₂ – d
Where x₂ is the position of equivalent lens.
Power of equivalent lens : – If the Power of first and second lenses are P₁ and P₂ respectively, then the Power of equivalent lens
P = P₁ + P₂ – dP₁P₂
Also read:- Deviation without Dispersion And Dispersion without deviation
Angle of Deviation , Refractive index of the Prism
Refraction of light at a spherical surface
Question 1. Find the position of the image formed by the lens combination given in the the figure.
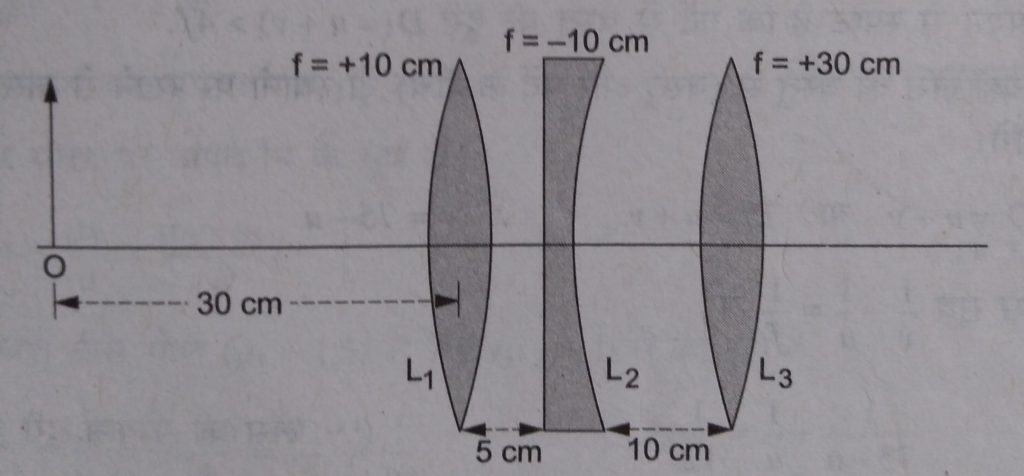
Solution.
Image formed by the first lens.
1/f₁ = 1/v₁ – 1/u₁
1/v₁ = 1/f₁ + 1/u₁ = 1/10 – 1/30 = ( 3 – 1 )/30 = 1/15
or v₁ = 15 cm
Image formed by the first lens serves as the object for the second lens. This is at ditance 15 – 5 = 10 cm for second lens.
f₂ = – 10
u₂ = 10
v₂ = ?
1/f₂ = 1/v₂ – 1/u₂
1/v₂ = 1/f₂ + 1/u₂ = 1/- 10 + 1/10 = 0/10
v₂ = infinite ( ∞ )
For the third lens.
f₃ = 30 cm
u₃ = ∞
v₃ = ?
1/v₃ = 1/f₃ + 1/u₃ = 1/30 – 1/∞
v₃ = 30 cm.
The final image is formed at 30 cm to the right of the third lens.











