Refraction of light at a convex surface :-
1. For real image :-
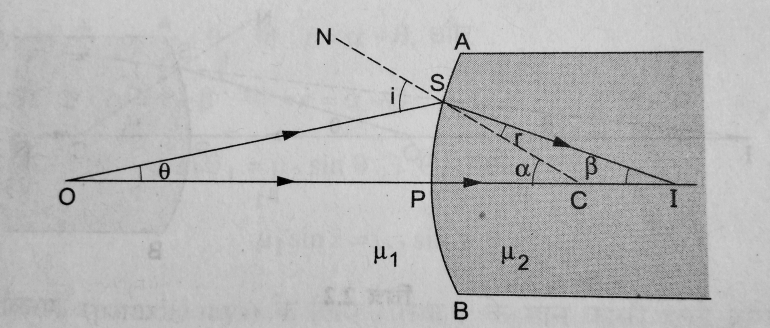
The figure shows the geometry of formation of image I of an object O on the principal axis of a spherical surface ( convex ) with centre of curvature C and radius of curvature R.
The rays are incident from a medium of refractive index μ₁ to another of refractive index μ₂.
Suppose that, ∠SCP = α, ∠SIP = β and ∠SOP = θ
Now, from ∆SOC, i = α +θ and from ∆ SCI, α = β + r
or r = α – β
Now, from Snell’s law
μ₁ sin i = μ₂ sin r
for paraxial rays-
μ₁ i = μ₂r
or μ₁ ( α + β) = μ₂ ( α – β )
or μ₁ ( SP/PC + SP/PO ) = μ₂ ( SP/PC – SP/PI )
or μ₁ ( 1/R + 1/-u ) = μ₂ ( 1/R – 1/v )
since, according to the sign convention u is negative, v and R are positive.
or μ₁/R – μ₁/u = μ₂/R – μ₂/v
Hence, μ₂/v – μ₁/u = ( μ₂ – μ₁ )/R
μ₁ = 1 ( Air ) and μ₂ = μ (Glass ), then
μ/v – 1/u = ( μ – 1 )/R
2. For virtual image :-
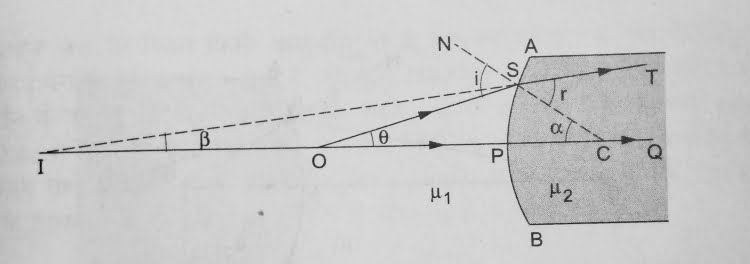
Let us consider, refractive index of medium 1 = μ₁
Refractive index of medium 2 = μ₂
Object distance PO = – u
Image distance PI = – v
Radius of curvature PC = +R
Angle of incident = i, angle of refraction = r
From the above figure,
In ∆ SOC, i = α + θ and in ∆SIC, r = α + β,
Now from Snell’s law
μ₁ sin i = μ₂ sin r
For paraxial rays, μ₁ i = μ₂ r
or μ₁ ( α + θ ) = μ₂ ( α + β )
or μ₁ ( SP/PC + SP/PO ) =μ₂ ( SP/PC + SP/PI )
μ₁ ( 1/R + 1/-u ) = μ₂ ( 1/R + 1/-v )
or μ₁/R – μ₁/u = μ₂/R – μ₂/v
Hence, μ₂/v – μ₁/u = ( μ₂ – μ₁ )/R
If μ₁ = 1 ( Air ) and μ₂ = μ ( Glass ), then
μ/v – 1/u = ( μ – 1 )/R
Refraction of light at a concave surface :-
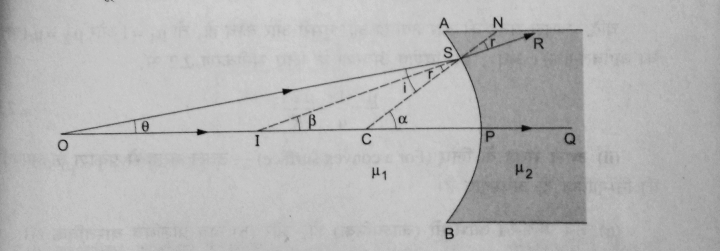
Let us consider, refractive index of medium 1 = μ₁
Refractive index of medium 2 = μ₂
Object distance PO = – u
Image distance PI = – v
Radius of curvature PC = – R
Angle of incident = i
Angle of refraction = r
From the above figure,
∠SCP = α, ∠SIP = β and ∠SOP = θ
Now, from ∆SOC, α = i + θ or i = α – θ and
from ∆SIC, α = r + β or r = α – β
Now, from Snell’s law
μ₁ sin i = μ₂ sin r
For paraxial rays, μ₁ i = μ₂ r
or μ₁ ( α -θ ) = μ₂ ( α – β )
or μ₁ ( SP/PC – SP/PO ) = μ₂ ( SP/PC – SP/PI )
or μ₁ ( 1/- R – 1/- u ) = μ₂ ( 1/- R – 1/- v )
or ₋ μ₁/R + μ₁/u = -μ₂/R + μ₂/v
Hence, μ₂/v – μ₁/u = ( μ₂ – μ₁ )/R
Numerical question-
- Light from a point source in air falls on a spherical glass surface ( μ = 1·5 and radius of curvature =20 cm ). The distance of the light source from the glass surface is 100 cm. At what position the image is formed ?
Solution.
μ₁ = 1 ( refractive index of air = 1 )
μ₂ = 1·5, R = 20 cm, u = – 100 cm
v = ?
μ₂/v – μ₁/u = ( μ₂ – μ₁ )/R
1·5/v + 1/100 = ( 1·5 – 1 )/20
1·5/v = 5/200 – 1/100 = ( 5 – 2 )/200 = 3/200
v = ( 1·5 x 200 )/3 = + 100 cm
Image formed at a distance of 100 cm in the direction of incident light.











