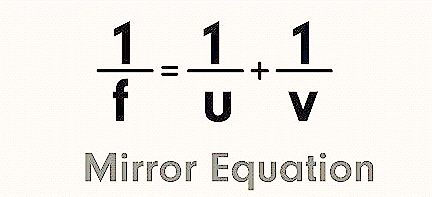The mirror equation :-
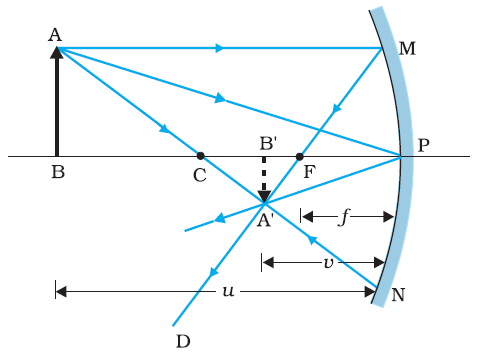
The ray diagram shows the image A’B’ of an object AB formed by a concave mirror .
We derive the mirror equation or the relation between the object distance (u), image distance (v) and the focal length (f).
From the above figure the two right angle triangle A’B’F and MPF are similar for paraxial rays MP can be considered to be a straight line perpendicular to CP therefore
A’B’/PM = B’F/FP
or B’A’/BA = B’F/PF ……….. eq (1)
since ( PM = AB )
∠APB = ∠A’PB’ the right angled triangles A’B’P and ABP are also similar, therefore
B’A’/BA = B’P/BP ………… eq (2)
Comparing eq. (1) and eq. (2), we get
B’F/FP = ( B’P – FP)/FP = B’P/BP ………… eq. (3)
equation (3) is a relation involving magnitude of distances.
We now apply the sign convention.
B’P = – v
FP = – f
BP = – u
Using these in equation (3) and we get
-v/-u = ( -v + f )/-f
or v/u = ( v – f )/f
or 1/f = 1/v + 1/u
This equation is known as the mirror equation.
Magnification :-
The linear magnification (m) as the ratio of the height of the image (h’) to height of the object (h)
That means m = h’/h
h’ and h will be taken nevative or postive in according to the sign convention.
In triagles A’B’P and ABP, we have
B’A’/BA = B’P/BP
With the sign convention, this becomes
-h/h = -v/-u
Thus, m = h’/h = -v/u
This equation is valid for all the cases of reflection by a spherical mirror (concave or convex) whether the image formed is real or virtual.
Some numerical questions.
Q. 1. An object is placed at (1) 10 cm (2) 5 cm in front of a concave mirror of radius of curvature 15 cm. Find the position, nature and magnification of the image in each case.
Solution.
(1) f = – 15/2 = -7·5 cm
u = -10 cm
v = ?
1/f = 1/v + 1/u
or 1/v = 1/f – 1/u
1/v = 1/⁻7·5 +1/-10 = ( -100 + 75 )/750 =-25/750 = -1/30
or v = -30 cm
the mirror on the same side as the object.
m = -v/u = – ( -30)/(-10 ) = -3
the image is magnified, real and inverted.
(2) u = -5cm
f = – 7·5 cm
1/f = 1/v + 1/u
1/v = 1/f – 1/u
1/v = – 10/75 + 1/5 = ( – 50 + 75 )/375
1/v = 25/375 = 1/15
or v = 15 cm.
the image is formed behind the mirror at 15 cm.
magnification
m = – v/u = -15/-5 = 3
the image is magnified, virtual and erect.
Q. 2. A 4·5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of the image and the magnification.
solution.
h = 4·5 cm
u = – 12 cm
f = 15 cm
v = ?
1/v = 1/f – 1/u = 1/15 + 1/12 = ( 4+5 )/60
V= 60/9= 6·7cm
Now,
h’/h=-v/u
h’=-v/u×h
=6•7/12×4•5
h’=2•5cm
m=h’/h
=2•5/4•5=5/9