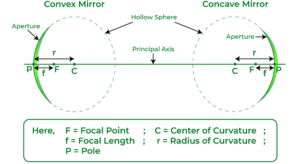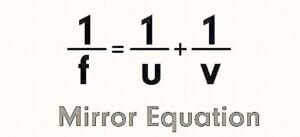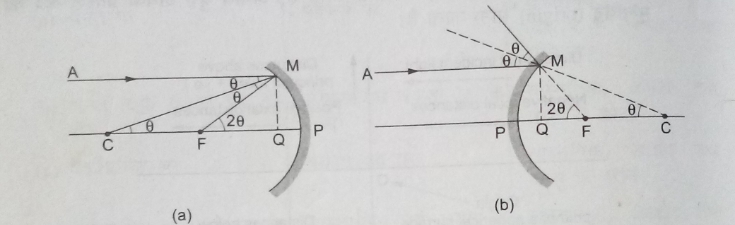
Let C be the centre of curvature of the mirror.
Consider a ray parallel to the principal axis strinking the mirror at M, CM will be perpendicular to the mirror at M.
Let θ be the angle of incidence and MQ be the perpendicular from M on the principal axis, then
∠MCP = θ and ∠MFP =2θ
Now
tanθ =MQ/CQ and tan2θ = MQ/FQ
for small θ, which is true for paraxial rays tanθ is aprox equal to θ and tan2θ is aprox equal to 2θ
Therefore from the above equation.
MQ/FQ = 2MQ/CQ
or FQ = CQ/2
Now, for small θ the point Q is very close to the point P therefore
FQ = f, CQ = R
Then from equation FQ = CQ/2
f = R/2
where f is focal length and R is radius of curvature.
Thus, In spherical mirror ( both concave and convex) focal length is equal to half of the radius of curvature.