Rate of a Chemical reaction :-
Some reactions such as ionic reactions occurs very fast , for example – precipitation of silver chloride occurs instantaneously by mixing of aqueous solutions of Silver nitrate and Sodium chloride .
Some reactions are very slow , for example – rusting of iron in the presence of air and moisture . Also there are reactions like inversion of Cane sugar and hydrolysis of starch , which proceed with a moderate speed or rate .
The rate of a Chemical reaction can be defined as the change in concentration of a reactant or product in unit time .
It can be expressed in in term of of –
1 . The rate of decrease in concentration of any one of the reactants .
2 . The rate of increase in concentration of any one of the products .
Consider a hypothetical reaction assuming that the volume of the system remains constant .
Reactant ( R ) → Product ( P )
One mole of the reactant produces one mole of the product .
If [ R ]₁ and [ P ]₁ are the concentrations of R and P respectively at time t₁ and [ R2 ]₂ and [ P2 ]₂ are their concentrations at time t₂ then
∆t = t₂ – t₁
∆[ R ] = [ R ]₂ – [ R ]₁
∆[ P ] = [ P ]₂ – [ P ]₁
The square brackets in the above expressions are used in express molar concentration .
Rate of disappearance of R = – decrease in concentration of R / time taken
= ∆ [ R ] / ∆t
Rate of appearance of P = + increase in concentration of P / time taken
= ∆ [ P ] / ∆t
Thus , Rate of a Chemical Reaction = – ∆ [ R ] / ∆t = + ∆ [ P ] / ∆t
Average rate of a Chemical reaction :-
Average rate depends upon the change in concentration of reactants or products and time taken for that change to occur .
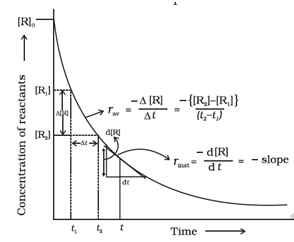
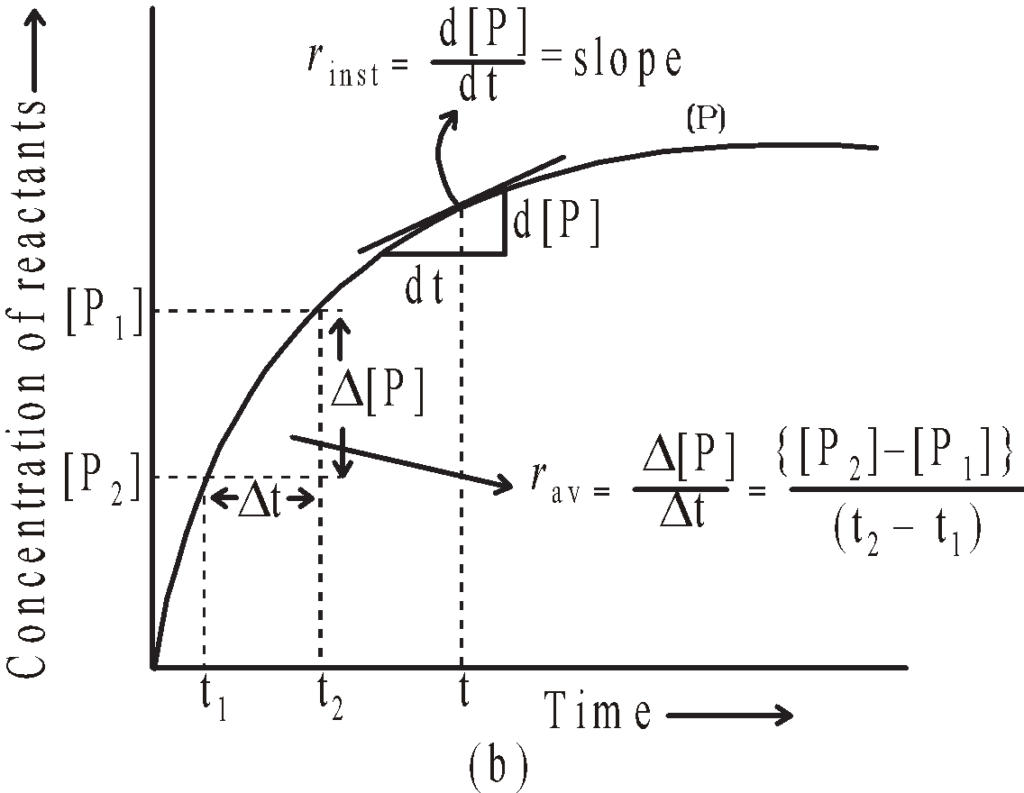
The average rate falls from 1.90 x 10⁻⁴ mol L⁻¹ s⁻¹ to 0.4 x 10⁻⁴ mol L⁻¹ s⁻¹ . Average rate cannot be used to predict the rate of a reaction at a particular instant as it would be constant for the time interval for which it is calculated .
The rate at a particular moment of time we determine the instantaneous rate . It is obtained at the smallest time interval
i . e . ∆t → 0
rᵢ = – d[ R ] / ∆t = + d[ P ] / dt
Or tanθ = rᵢ
The instantaneous rate of a Chemical reaction is the slope of the line ( the tangent to Curve ) at any time dt .
Average rate of reaction
rₐ = – ∆[ R ] / ∆t = ∆[ P ] / dt
Units of rate of a chemical reaction :-
Units of rate are concentration time ⁻¹
Example – If concentration is in mole L⁻¹ and time is in second then the units will be mole L⁻¹ s⁻¹
When the concentration of gases is expressed in terms of their partial pressures , then the units of the rate of equation will be atm s⁻¹
- Now consider a reaction
Hg ( l ) + Cl₂ ( g ) → HgCl₂ ( s )
Where stoichiometric coefficients of the reactants and products are same , then rate of the reaction is given as
Rate of reaction = – ∆ [ Hg ] / ∆t = – [ Cl₂ ] / ∆t
= ∆ [ HgCl₂ ] / ∆t
In the following reaction two moles of HI decomposed to produce one mole each of H₂ and I₂
2 HI ( g ) → H₂ ( g ) + I₂ ( g )
Since the rate of consumption of HI is twice the rate of formation of H₂ or I₂ to make them equal , the term ∆ [ HI ] is divided by 2 .
The rate of this reaction is given by
Rate of reaction = – 1 / 2 ∆ [ HI ] / ∆t = ∆ [ H₂ ] / ∆t = ∆ [ I₂ ] / ∆t
- Similarly for the reaction –
5 Br⁻ ( aq ) + BrO₃⁻ ( aq ) + 6 H⁺ ( aq ) →3 Br₂ ( aq ) + 3 H₂O ( l )
Rate of a Chemical reaction = – 1 / 5 ∆ [ Br⁻ ] / ∆t = ∆ [ BrO₃⁻ ] / ∆t = – 1 / 6 ∆ [ H⁺ ] / ∆t = 1 / 3 ∆ [ Br₂ ] / ∆t
= 1 / 3 ∆ [ H₂O ] / ∆t
- For a gaseous reaction at constant temperature , concentration is directly proportional to the partial pressure of a species and hence , rate can also be expressed as rate of change in partial pressure of the reactant or the product .
Factors influencing Rate of a Chemical reaction :-
Rate of a Chemical reaction depends upon the experimental conditions such as concentration of reactants ( pressure in case of gases ) , temperature and catalyst .
Dependence of rate on Concentration :-
The rate of a chemical reaction at given temperature many dependent on the concentration of one or more reactants or products .The rate of a Chemical reaction decreases with the the passage of time as the concentration of reactants decrease . Conversely rate generally increase when reactant concentration increase . So , rate of reaction depends upon the concentration of reactants .
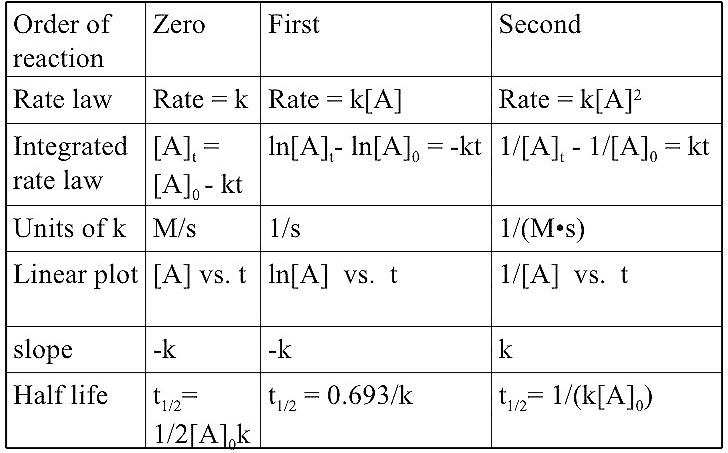
It is known as Rate Law .
Consider a General reaction
aA + bB → cC + dD
Where a , b , c and d are the stoichiometric coefficients of reactants and products .
The rate expression for this reaction is
Rate α [ A ]ˣ [ B ]ʸ
Or Rate = K [ A ]ˣ [ B ]ʸ
Where K is rate constant .
Or
– d[ R ] / dt = K [ A ]ˣ [ B ]ʸ
Thus , rate law is the expression in which reaction rate is given in terms of molar concentration of reactants with each term raised to some Power , which may or may not be same as the stoichiometric coefficient of the reacting species in a balanced Chemical equation .
Example – 2NO ( g ) + O₂ ( g ) → 2NO₂ ( g )
The rate equation for this reaction will be
Rate = K [ NO ]² [ O₂ ]
The differential form of this rate expression is given as
- – d[ R ] / dt = K [ NO ]² [ O₂ ]
Temperature dependence of the Rate of a Chemical reaction :-
Most of the Chemical reactions are accelerated by increase in temperature .
Example – In decomposition of N₂O₅ ,the time taken for half of the original amount of material to decompose is 12 minutes at 50⁰C , 5 hours at 25⁰C and 10 days at 0⁰C .
It has been found that for a Chemical reaction with rise in temperature by 10⁰C , the rate constant is nearly double .
- The temperature dependence of the rate of a Chemical reaction can be accurately explained by Arrhenius equation –
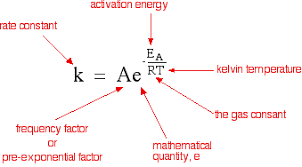
Where A is the Arrhenius factor for frequency factor . It is a constant specific to a particular reaction . R is gas constant and Eₐ is activation energy measured in joules per mole .
It can be understood clearly using the following simple reaction –
H₂ ( g ) + l₂ ( g ) → 2HI ( g )
According to Arrhenius , this reaction can take place only when a molecule of hydrogen and a molecule of iodine collide to form and unstable intermediate .
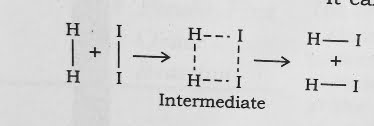
It exists for a very short time and then breaks up to form two molecules of hydrogen iodide .
The energy required to on this intermediate called activated complex ( C ) is known as activation energy Ea .
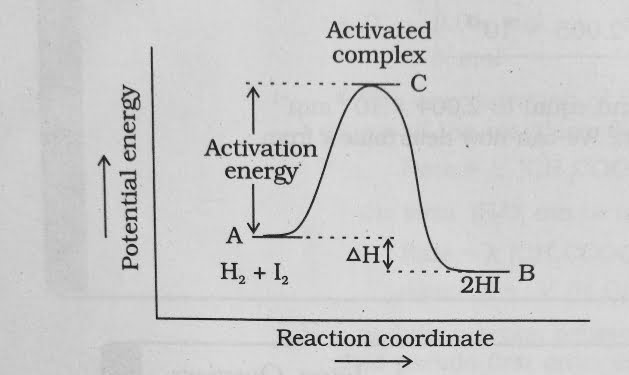
The above figure is obtained by plotting potential energy Vs reaction Coordinate .
Reaction coordinate represents the profile of energy change when reactants change into products .
- some energy is released when the complex decomposes to form products . So , the final heat of the reaction depends upon the nature of reactants and products .
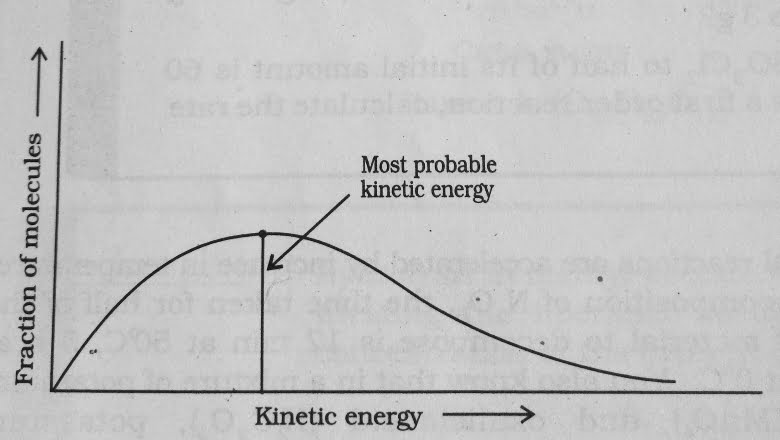
- All the molecules in the reacting species do not have the same kinetic energy . According to Boltzmann and James clerk Maxwell , the distribution of kinetic energy may be described by plotting the fraction of molecules with a given kinetic energy ( E ) vs kinetic energy .
Effect of Catalyst :-
A catalyst is a substance which increases the rate of a Chemical reaction without itself undergoing any permanent chemical change .
Example – KClO₃ + MnO₂ → 2KCl + 3O₂
Where MnO₂ is a catalyst . The word catalyst should not be used when the added substance reduces the rate of a Chemical reaction .
- A small amount of the catalyst can catalyse a large amount of reactants . A Catalyst does not alter Gibs energy , ∆ G of a reaction . It Catalyses spontaneous reaction only .
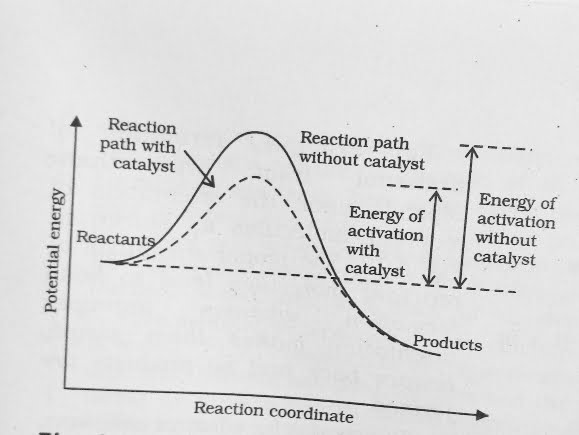
- It is believed that the catalyst provides an alternate pathway for reaction mechanism by reducing the activation energy between reactants and products and hence lowering the potential energy barrier .
- It is clear from Arrhenius equation that lower the value of activation energy faster will be the rate of reaction .
Molecularity of a reaction :-
The number of reacting species ( atoms , ions or molecules ) taking part in an elementary reaction , which must collide simultaneously in order to bring about a chemical reaction is called molecularity of a reaction .
Examples –
1 . N₂O₅ → N₂O₄ + 1 / 2 O₂
Order = 1
Molecularity = 1
2 . 2HI → H₂ + I₂
Order = 2
Molecularity = 2
3 . 2NO + O₂ → 2NO₂
Order = 3
Molecularity = 3
- Unimolecular reaction involves one reacting species , biomolecular reaction involves simultaneously collision between two species .
Trimolecular or tetramolecular reaction involves simultaneous collision between three reacting species .
Order of Reaction :-
The sum of powers of the concentration of the reactants in the rate law expression is called the order of that chemical reaction .
Example – Rate of reaction = K [ A ]ˣ [ B ]ʸ
Here x and y represent the order with respect to the reactants A and B respectively . Sum of these components i . e . x + y give the overall order of a reaction .
Order of a Chemical reaction can be 0, 1, 2, 3 and even a fraction . A Zero order reaction means that the rate of a Chemical reaction is in dependence of the concentration of reactants .
Collision theory of Chemical Reactions :-
Collision theory states that for a Chemical reaction to occur , the reacting particles must collide with one another . It is based on kinetic theory of gases .
- The rate of reaction depends on the frequency of collisions . The theory also tells us that reacting particles often collide without reacting .
For Collision to the successful , reacting particles must collide with sufficient energy and with the proper orientation . The collision is called effective collision .
- The number of collisions per second per unit volume of the reaction mixture is known as collision frequency ( Z ) .
Example – A + B → Product .
Rate = Z e⁻ Eₐ / RT
Where Z represents the collision frequency of reactants , A and B and e ⁻ Eₐ / RT represents the fraction of molecules with energies equal to or greater than activation energy ( Eₐ )
For example , formation of methanol from Bromoethane depends upon the orientation of reactant molecules .
The proper orientation of reactant molecules lead to bond formation where as improper their orientation makes them simply bounce back and no products are formed .
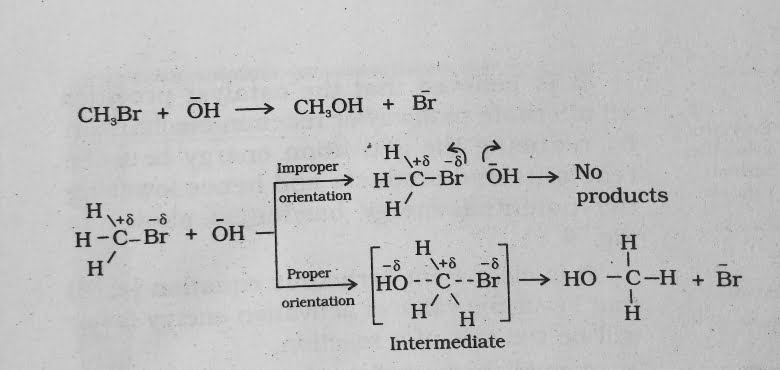
- In collision theory activation energy and proper orientation of the molecules together determine the criteria for an effective collision and hence the rate of a chemical reaction .
- Collision theory also has certain drawbacks as it considers atoms / molecules to be hard spheres and ignores their structural aspect .