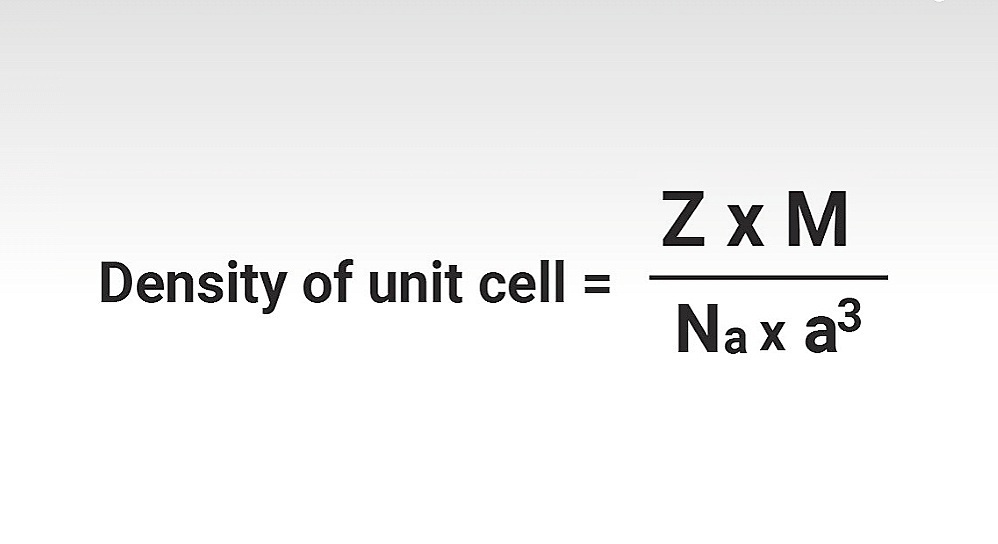Theoretical Density :-
Knowing the unit cell dimensions, the theoretical density d of a cubic crystal can be calculated from the equation
d = Z M / N V
where Z is the number of atoms in the unit cell, M is the molar mass, V is the volume of the unit cell and N is the Avogadro constant.
Suppose, edge length of a unit cell of a cubic crystal determined by X – ray diffraction is a, then
d = Z M / a³ N
The theoretical density obtained using the above equation is with the assumption that each lattice point is occupied by the species. But if some lattice points remain vacant, percentage occupancy can be calculated from the experimental density ( d₁ ) and the theoretical or calculated density ( d ₂ )
percentage occupancy = d₁ / d₂ x 100
Problems :-
- Silver forms FCC lattice and x-ray studies of its crystals show that the edge length of its unit cell is 408·6 pm. Calculate the density of silver ( Atomic mass = 107·94 ).
solution.
Since, silver forms FCC lattice.
Hence, the number of silver atoms per unit cell ( Z ) = 4
M = 107·9 g mol⁻¹ = 107·9 x 10⁻³ kg mol⁻¹
a = 408·6 pm = 408·6 x 10⁻¹² m
d = ?
d = Z M / a³ N
= 4 x 107·9 x10⁻³ / ( 408·6 x 10⁻¹² )³ x 6·022 x 10²³
= 10·5 x 10³ kg m⁻³
= 10·5 g cm⁻³
2 · Silver crystallises in FCC lattice, if edge length of the cell is 4·07 x 10⁻⁸ cm and density is 10·5 g cm⁻³, calculate the atomic mass of silver.
Solution.
For silver FCC lattice, Z = 4
a = 4·07 x 10⁻⁸ cm
d = 10·5 g cm⁻³
N = 6·022 x 10²³ atom mol⁻¹
d = Z M / a³ N
M = d a³ N / Z = 10·5 x ( 4·07 x 10⁻⁸ )³ x 6·022 x 10²³ / 4
= 4262·97 x 10²³ / 4 x 10²⁴
= 106·57 u
3. Lithium has a bcc structure. Its density is 530 kg m⁻³ and its atomic mass is 6·94 g mol⁻¹, calculate the edge length of a unit cell of lithium metal.
Solution.
d = 530 kg m⁻³ = 0·53 g cm⁻³
M = 6·94 g mol⁻¹
N = 6·02 x 10²³ mol⁻¹
For bcc, Z = 2
a = ?
d = Z M / a³ N
a = ₃√Z M / ₃√d N
a = ₃√2 x 6·94 / ₃√0·53 x 6·02 x 10²³ cm⁻³
a = ₃√4·35 x 10⁻²³ cm⁻³
a = 3·52 x 10⁻⁸ cm
352 pm