Atomic radius, Packing fraction and Empty space in the Close Packing

Atomic radius :-

• In a Simple or primitive cubic unit cell, the two adjacent corner atoms are supposed to touch each other along the edge of the cube.

Thus, the edge length or side of the cube a and the atomic radius of each particle r are related as

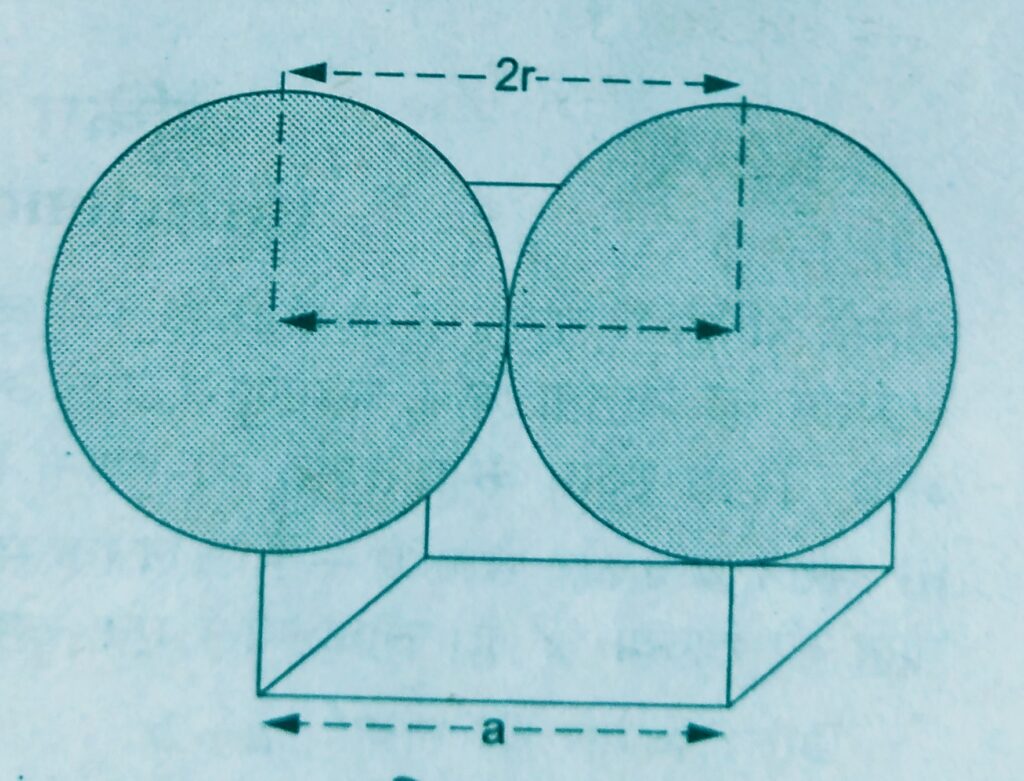
a = 2 r

r = a / 2

• In a body centred cubic cell ( bcc ), the atom at the centre of the cube is suppose to touch the corner atoms diagonally.

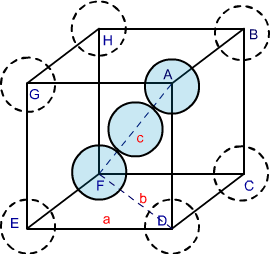
In ∆ EFD,

b² = a² + a² = 2a

b = √2 a

Now in ∆ AFD

c² = a² + b² = a² + 2 a² = 3 a²

c = √3 a

The length of the body diogonal c = 4 r

Where r is the atomic radius of the atom ( sphere ) as all the three spheres along the diagonal touch each other.

Therefore,

√3 a = 4 r

a = 4 r / √3

r = √3 a / 4

• In a face centred cubic cell (FCC ) or CCP, the atom at the face centre is supposed to touch its adjacent corner atoms.

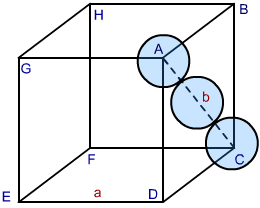
Let the unit cell edge length = a,

face diagonal AC = b

In ∆ ABC

AC² = BC² + AB²

b² = a² + a²

b = √2a² = √2 a

If r is the atomic radius of the sphere, we find

b = 4 r = √2 a

or a = 4 r / √2 =2 √2 r

r = a / 2 √2

Packing fraction and Empty space in the close packing :-

• In a simple cubic cell, there is only one atom per unit cell. Volume of the atom = 4 π r³ / 3 = 4 π / 3 ( a / 2 )³ = π a³ /6

Volume of one unit cell = a³

Hence, packing fraction = π a³ / 6 a³ = π / 6 = 0·5236 = 52·36 %

Percentage of vacant space = ( 100 – 52·36 ) % = 47·64 %

• In a body centred cubic cell, there are two atoms per unit cell.

Volume of two atoms = 2 x ( 4 π r³ / 3 )

= 2 x 4 π / 3 x ( √3 a / 4 )³

= √3 π a³ / 8

Hence, packing fraction = √3 π a³ / 8 a³ = √3 π / 8 = 0·6802 = 68·02 %

Percentage of vacant space = ( 100 – 68·02 ) = 31·98 %

• In a face Centred Unit Cell, there are four atoms per unit cell.

Volume of four atoms = 4 x ( 4πr³ / 3 )

= 4 x 4 π / 3 x ( √2 a / 4 )³ = √2 π a³ / 6

Hence, packing fraction = √2 π a³ / 6 a³ = √2 π / 6 = 0·7406 = 74·06 %

Percentage of vacant space = ( 100 – 74·06 ) % = 25·94 %

Problems :-

1. Lithium metal crystallises in a body centred cubic ( bcc ) crystal. If the length of the side of the unit cell of lithium is 431 pm, the atomic radius of the lithium will be –

Solution.

a = 351 pm

r = ?

r = √3 a / 4

r = √3 x 351 / 4 = 151·98 pm.

2. The edge length of face centred unit cubic cell is 508 pm, If the radius of the cation is 110 pm, the radius of the anion is –

Solution.

a = 2 ( r⁺ + r⁻ )

r⁺ + r⁻ = a / 2

r⁻ = (a / 2 ) – r⁺ = ( 508 / 2 ) – 110 = 144 pm