In Crystals, the constituent particles are close packed and leaving the minimum vacant space. In such a situation, the entropy of crystalline material becomes minimum.
Let us consider the constituent particles as identical hard spheres and build up three dimensional structure in following three steps –
Close Packing in one Dimension :-

There is only one way of arranging spheres in a one dimensional close packed structure. In this arrangement, each sphere is in contact with two of its neighbours.
The number of nearest neighbours of particle is called its coordination number.
Thus, in one dimensional close packing arrangement, the coordination number is 2 .
2. Close Packing in two Dimensions :-
It can be generated by placing the rows of close packed spheres in two different ways –
( a ) X X X – types arrangement of rows :-
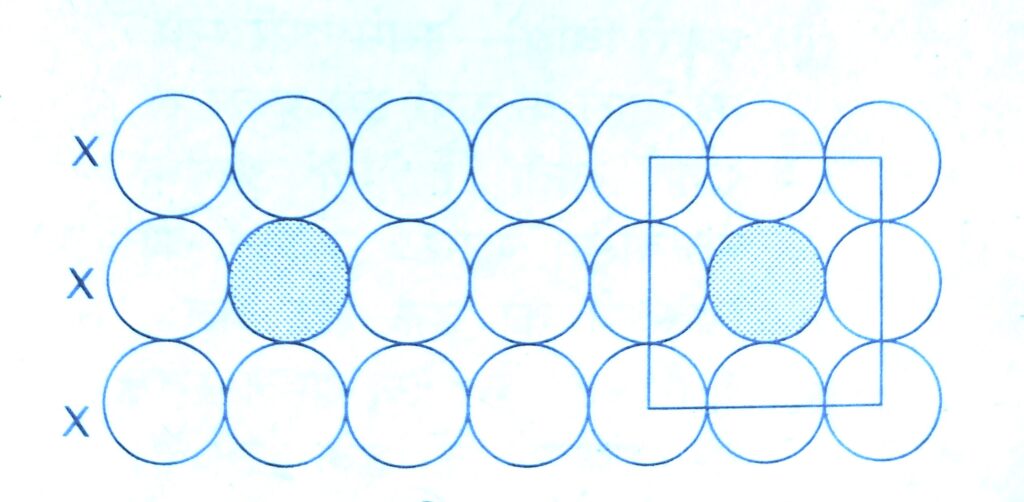
In this packing the second row may be placed in contact with the first one such that the spheres of the second row are exactly above those of the first row. This arrangement is also called square close packing.
In this arrangement each sphere is in contact with four of its neighbours. Thus the two dimensional coordination number is 4.
( b ) X Y X – type arrangement of rows :-
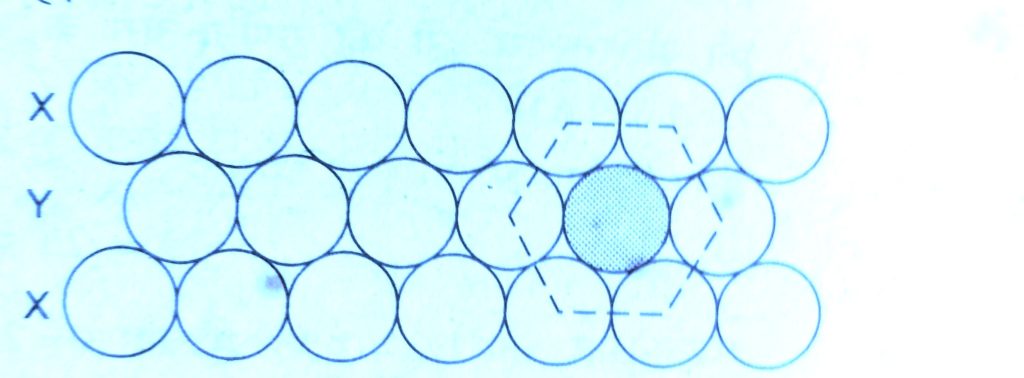
In this packing the second row may be placed above the first one in a staggered manner such that its spheres fit in the despression of the first row.
In this arrangement there is less free space. This arrangement is also called hexagonal close packing.
Each sphere is in contact with six of its neighbours, therefore the two dimensional coordination number is 6.
3. Close packing in three Dimensions :-
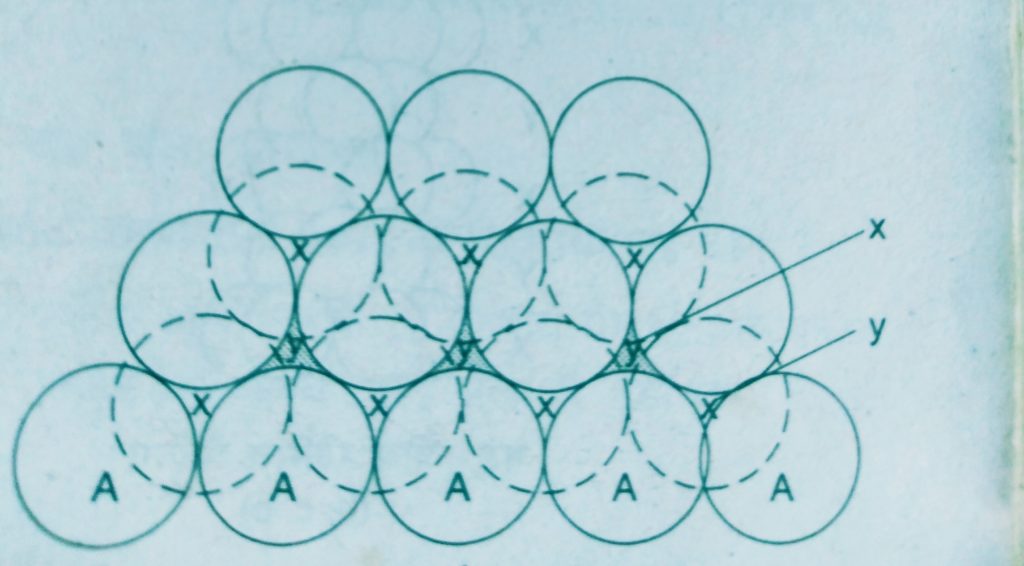
Three dimensional close packing can be obtained from two dimensional square close packed layers and two dimensional hexagonal close packed layers
- Placing the second square packed layer above the first. The second layer is placed over the first layer such that the spheres of the upper are exactly above those of the first layer.
If the arrangement of spheres in the first layer is called A – type, all the layers have the same arrangement. Thus this lattice has AAA – type pattern. The lattice generated is the simple cubic lattice and its unit Cell is the primitive cubic unit cell.
- A two dimensional hexagonal close packed layer and place a similar layer above it such that the spheres of the second layer are placed in the depressions of the first layer.
This gives rise the different arrangements.
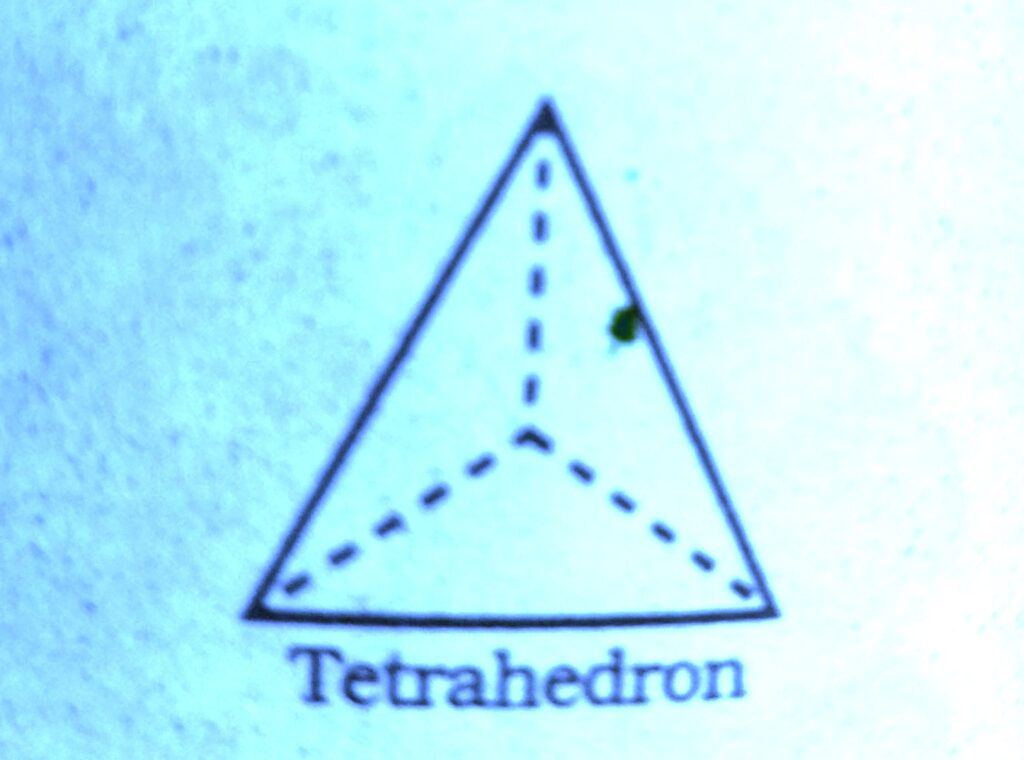
Wherever a sphere of the second layer is above the void of the first a tetrahedral void is formed, these voids are called tetrahedral voids because a tetrahedron is formed when the centres of these four spheres are joined.
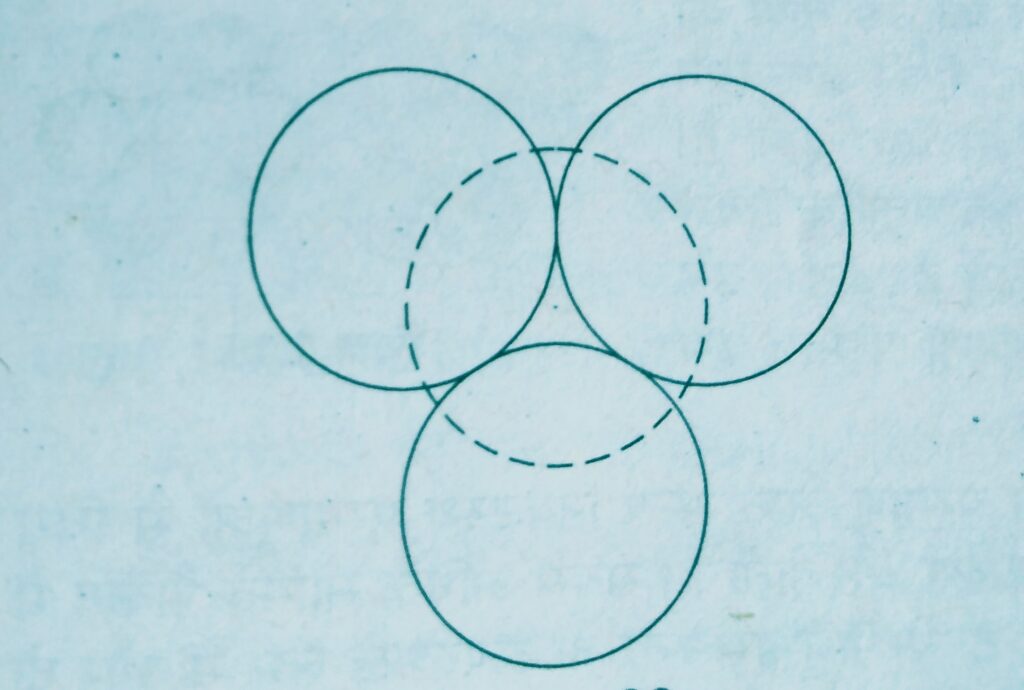
At the other places the triangular voids in the second layer are above the triangular voids in the first layer and the triangular shapes of these do not overlap.
Such voids are surrounded by six spheres and are called octahedral voids.
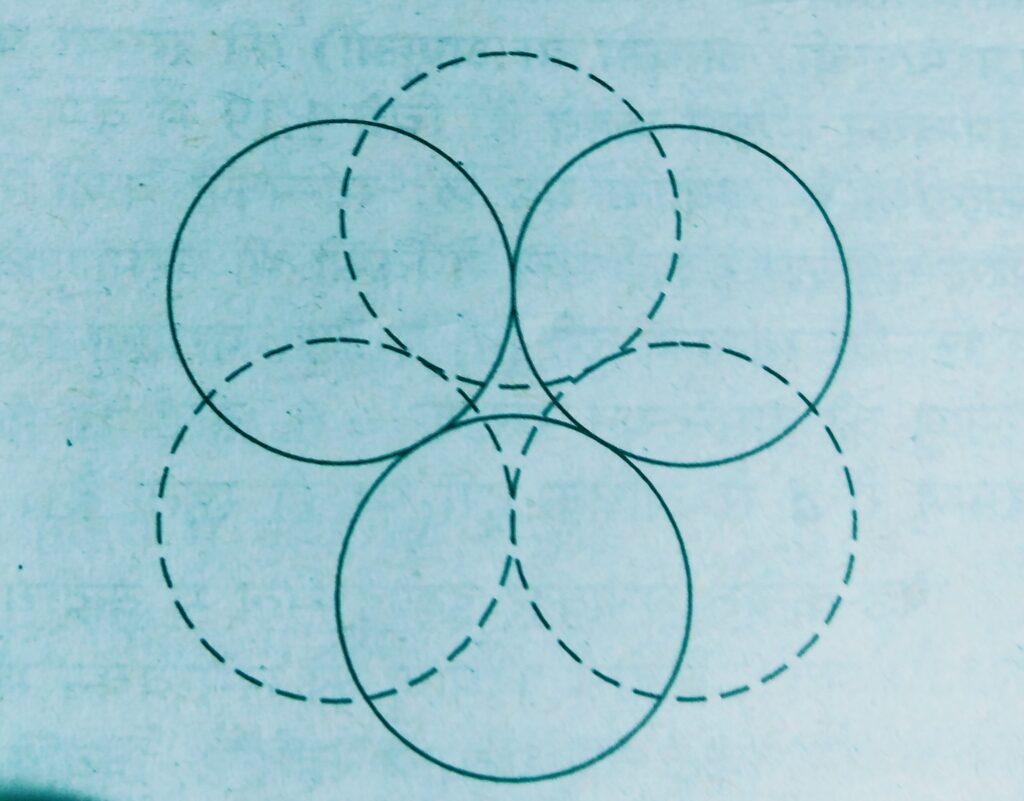
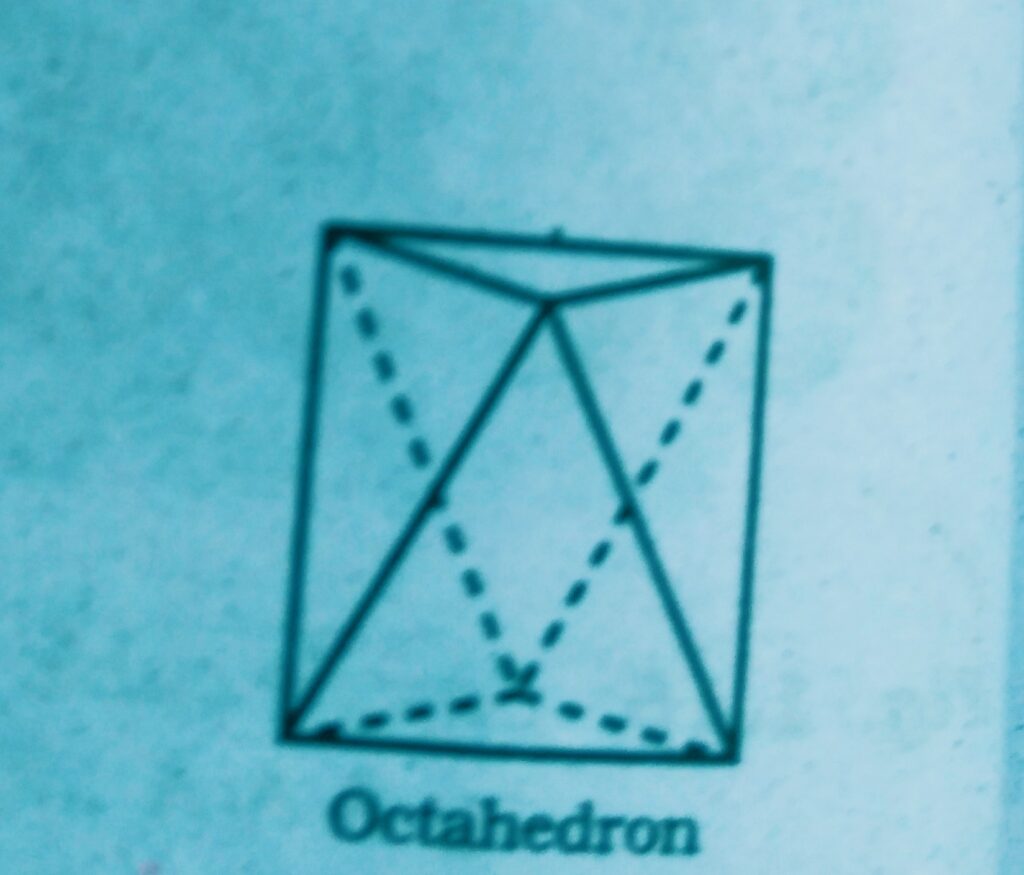
- If the number of close packed spheres be N then the number of octahedral voids = N
The number of tetrahedral voids = 2N
Placing third layer over the second layer :- when third layer is placed over the second, there are two possibilities –
- Covering tetrahedral voids :- Tetrahedral voids of the second layer may be covered by the third layer. In this case the spheres of the third layer are exactly aligned with those of the first layer. Thus the pattern of spheres is repeated in alternate layers that means XYXY – pattern. This structure is called hexagonal close packed ( hcp ) stucture.
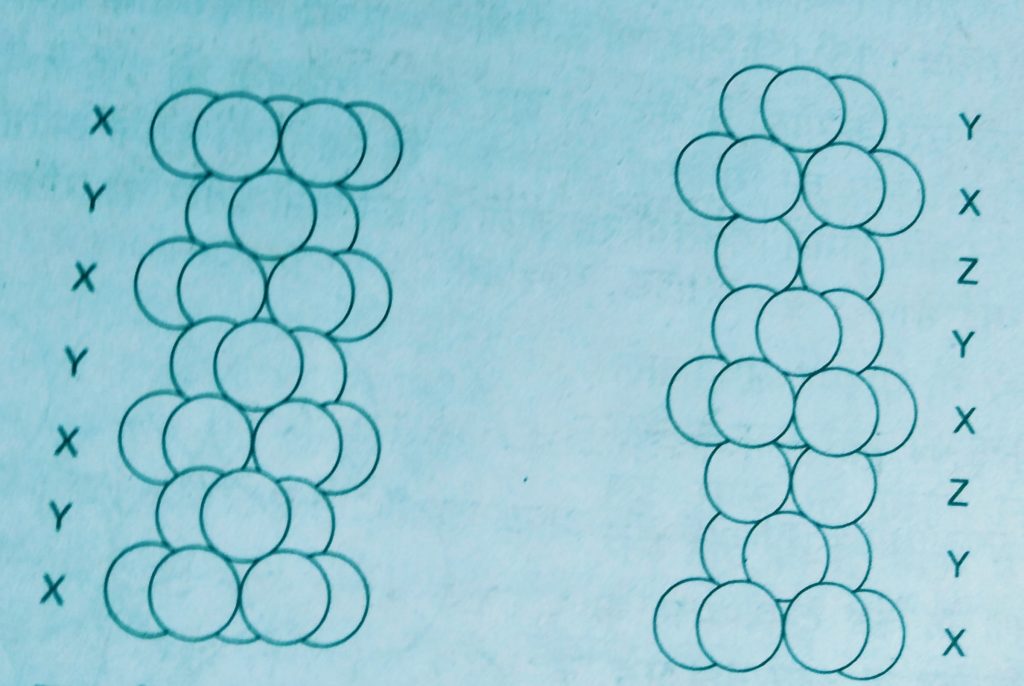
Examples. – Mg and Zn crystals are in this structure.
2. Covering octahedral voids :- The third layer may be placed above the second layer in a manner such that its spheres over the octahedral voids. When placed in this manner , the spheres of the third layer are not aligned with those of either the first or second layer.
This arrangement is called C type. Only when fourth layer is placed, its spheres are aligned with those the first layer. This pattern of layers is written XYZ XYZ …….
This structure is called Cubic Close Packed ( C C P ) or ( F C C ).
Examples. – copper and silver crystallise in this structure.
In both types of close packing structures h c c p and c c p, each sphere is in contact with twelve spheres. Thus the coordination number is 12.